Assume-Guarantee Abstraction Refinement in SpaceEx
Contents
Overview
Supporting material for the paper "Assume-Guarantee Abstraction Refinement Meets Hybrid Systems" [1], 10th Haifa Verification Conference HVC2014.
Large systems consisting of multiple components pose a special challenge for verification algorithms. Compositional verification techniques in the assume-guarantee style have been successfully applied to transition systems to efficiently reduce the search space by leveraging the compositional nature of the systems under consideration. We adapt these techniques to the domain of hybrid systems with affine dynamics. To build assumptions we introduce an appropriate abstraction based on location merging. We integrate the assume-guarantee style analysis with automatic abstraction refinement. We have implemented our approach in the symbolic hybrid model checker SpaceEx. The evaluation shows its practical potential. To the best of our knowledge, this is the first work combining assume-guarantee reasoning with automatic abstraction-refinement in the context of hybrid automata.
Assume-guarantee reasoning is a well-known methodology for the verification of large systems. The idea behind is to decompose the verification of a system into the verification of its components, which are smaller and therefore easier to verify. The most challenging part of applying assume-guarantee reasoning is coming up with appropriate assumptions to use in the application of abstraction-refinement techniques for automating the generation of assumptions for the verification of transition systems.
In this paper, we focus on the automated generation
of assumptions in the context of hybrid systems. We
use abstraction-refinement techniques to iteratively
build the assumptions needed to perform
assume-guarantee reasoning. Let us consider a system
consisting of two components
(plant) and 
(controller). We check whether the
composed system satisfies a given property
. In
scope of our compositional reasoning framework, we
first abstract the controller
by
its over-approximation
. If the property is not violated in
the composition of and
, then we can immediately conclude
that also the original system is safe. Otherwise, we
obtain a counterexample leading to an abstract error
state. Our algorithm proceeds with the analysis of
the found counterexample. If it is spurious, the
abstraction is refined to eliminate
it. If the counterexample is genuine, then the
parallel composition
violates .
We present a framework which can efficiently handle the class of affine
hybrid systems. Due to the mixed discrete-continuous nature of hybrid
systems, we need to pay special attention on the abstraction of
continuous dynamics. We illustrate the idea of our compositional
analysis on a toy example. Fig. 1 shows a simple hybrid automaton
consisting of the plant and controller .
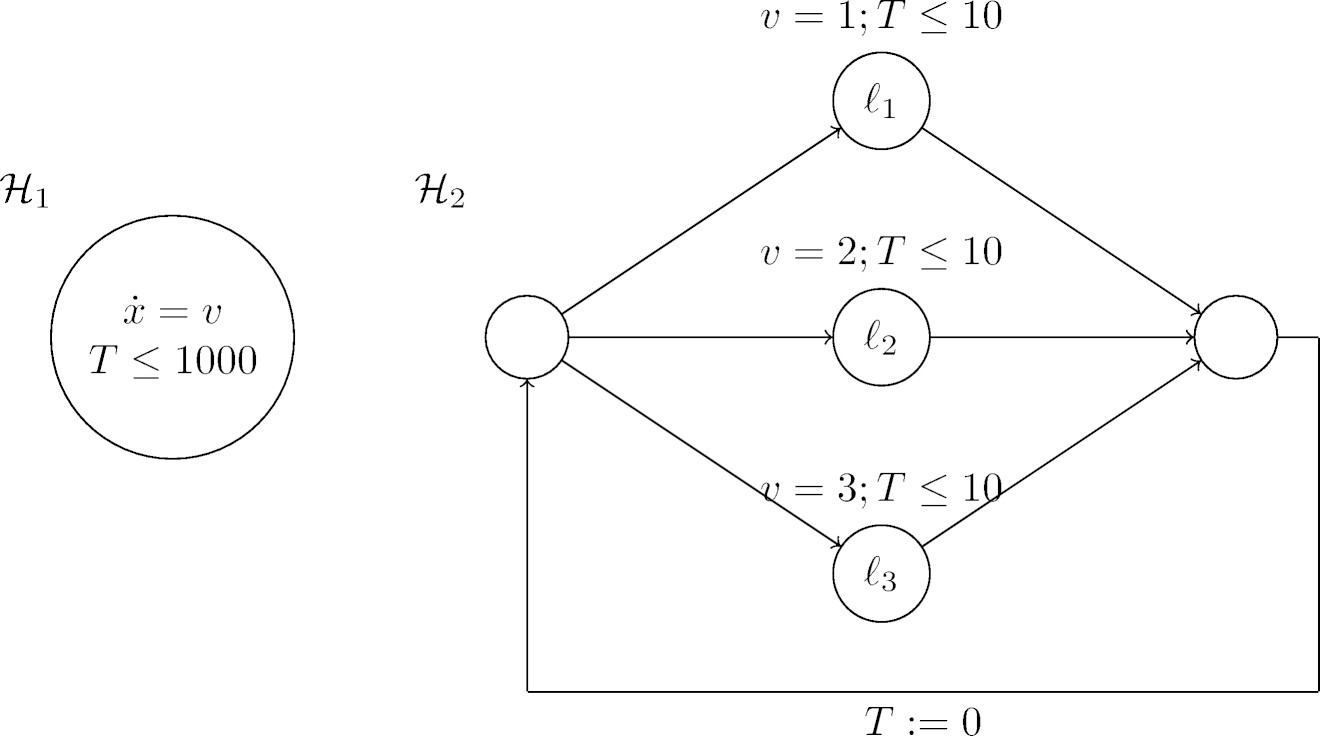
Fig. 1: A motivating example - unmerged.
We observe that the derivative of variable 
in plant depends on the value of 
governed by the controller . Furthermore, we see that the controller operates
in iterations of length 10. The possible controller options are grouped
in a stratum. While analyzing this system, a hybrid model checker will
consider all the three options on every controller iteration which
results in 
branches
for 
iterations. By noting
that for some properties only the minimal and maximal values of are of relevance, we come up with
an abstracted version of the automaton in Fig. 2.
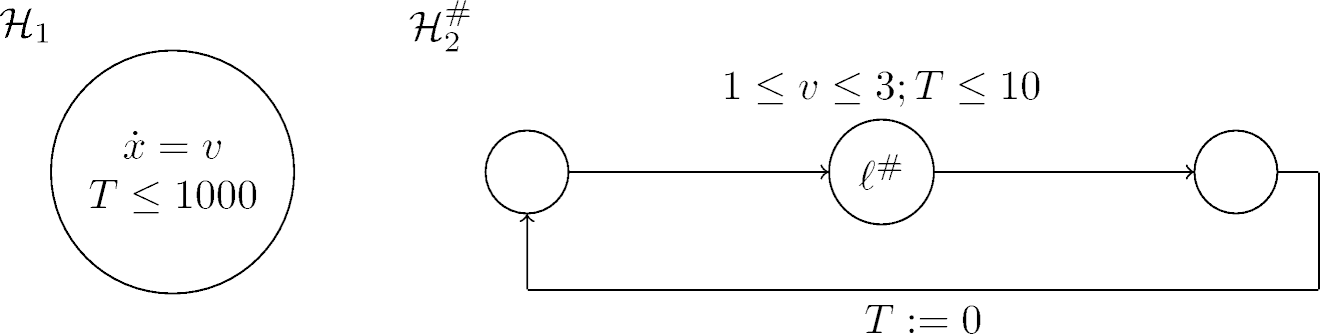
Fig. 2: A motivating example - merged.
We replace the three alternative options by only
one coarser option. To ensure that the
resulting automaton is indeed an over-approximation
of the original system, we use
as an invariant of the merged location
,
i.e., we replace the exact values of
with its
bounds. This abstraction will be especially useful
to prove, e.g., that within the first 1000 seconds
of controller operation the state
will still not be reached. In the
abstraction we will reduce an exponential number of
branchings to a linear one. Note that this kind of
location-merging abstractions is especially useful
for the class of stratified controllers,
i.e. consisting of multiple layers. The reason is
that the controller structure can be exploited to
efficiently generate an initial abstraction by
merging locations belonging to the same
strata. Intuitively, this step allows us to adjust
the precision level at which the system parameters
are taken into account. If the resulting abstraction
is too coarse, then the finer grained abstraction is
generated in the refinement step.
The lesson we learn from this example is that merging of
locations is a promising approach to generate abstractions in
scope of the assume-guarantee reasoning paradigm. To ensure
the conservativeness of the resulting abstraction, we compute
the invariants as a convex hull of the original locations.
Note that the computation of minimal and maximal values of
shown above
represents a simple case of a general convex hull
computation. Given the continuous, affine dynamics of the
form 
, the merged locations are computed by first
eliminating the (unprimed) state variables and consequently
computing the convex hull of the resulting polytopes over the
derivatives. Our implementation in SpaceEx shows the
practical potential.
Download
Click here to download the archive which has the following contents:
- 64-bit binaries of SpaceEx supporting AGAR with the necessary libraries
- Models of plants and controllers
- Scripts to run each sample
For more information, please contact Sergiy Bogomolov or Marius Greitschus.
References
- Sergiy Bogomolov, Goran Frehse, Marius Greitschus, Radu Grosu, Corina Pasareanu, Andreas Podelski, and Thomas Strump. "Assume-Guarantee Abstraction Refinement Meets Hybrid Systems", HVC2014 [ springer | dblp | pdf ].